L1 趋势滤波 —— 简介及Python实现

近期在研究量化，试图基于趋势构建一个可学习的行情评估指标作为因子使用

查找过较多资料后初步期望通过L1趋势滤波来实现原始数据集的生成

既然希望了解那就了解个全面，顺便复习一下久违的运筹学，遂向AI请教以补全该文章

‍

注：本文为AI协助生成，若不够准确还请勘误

1. 引言

L1 趋势滤波是一种重要的信号处理方法，它能够有效地从含噪信号中提取趋势成分。与传统的滤波方法相比，L1 趋势滤波具有保持信号突变特征的优势，这使其在多个领域得到广泛应用。

2. 数学问题形式化

2.1 基本问题描述

L1 趋势滤波的核心是解决如下优化问题：

$$\min_{x} \frac{1}{2}||x - y||_2^2 + \lambda||Dx||_1$$

其中：

$x$ 是要提取的趋势信号
$y$ 是原始观测信号
$D$ 是二阶差分矩阵
$\lambda$ 是正则化参数

2.2 二阶差分矩阵

对于长度为 n 的信号，二阶差分矩阵 D 的形式为：

$$D = \begin{bmatrix}
1 & -2 & 1 & 0 & \cdots & 0 \\
0 & 1 & -2 & 1 & \cdots & 0 \\
\vdots & \ddots & \ddots & \ddots & \ddots & \vdots \\
0 & \cdots & 0 & 1 & -2 & 1
\end{bmatrix} \in \mathbb{R}^{(n-2)\times n}$$

3. 问题转化与求解

3.1 引入辅助变量

由于 L1 范数不易直接优化，引入辅助变量 v，将问题转化为：

（其中辅助变量用于表达差分的上界，限制变化幅度，用于将实际问题转化为最优化范围内的问题）

$$\begin{aligned}
\min_{x,v} & \quad \frac{1}{2}||x - y||_2^2 + \lambda\sum_i v_i \\
s.t. & \quad -v \leq Dx \leq v
\end{aligned}$$

3.2 拉格朗日对偶问题

构建拉格朗日函数（将约束转化至求解方程内）：

$$L(x,v,\mu_1,\mu_2) = \frac{1}{2}||x - y||_2^2 + \lambda\sum_i v_i + \mu_1^T(Dx - v) + \mu_2^T(-Dx - v)$$

3.3 标准二次规划形式

将拉格朗日函数转化为标准二次规划问题：

$$\begin{aligned}
\min_{z} & \quad \frac{1}{2}z^TPz + q^Tz \\
s.t. & \quad Gz \leq h
\end{aligned}$$

3*. 拉格朗日函数转标准二次规划过程推导

1. 原始优化问题

首先写出原始问题：

$$\begin{aligned}
\min_{x,v} & \quad \frac{1}{2}||x - y||_2^2 + \lambda\sum_i v_i \\
s.t. & \quad -v \leq Dx \leq v
\end{aligned}$$

2. 构建拉格朗日函数

将不等式约束改写为：

$$Dx - v \leq 0 \text{ 和 } -Dx - v \leq 0$$

引入拉格朗日乘子$\mu_1, \mu_2 \geq 0$，得到拉格朗日函数：

$$L(x,v,\mu_1,\mu_2) = \frac{1}{2}||x - y||_2^2 + \lambda\sum_i v_i + \mu_1^T(Dx - v) + \mu_2^T(-Dx - v)$$

3. 最优性条件

3.1 对 x 求导：

$$\frac{\partial L}{\partial x} = (x - y) + D^T(\mu_1 - \mu_2) = 0$$

整理得：

$$x = y - D^T(\mu_1 - \mu_2)$$

3.2 对 v 求导：

$$\frac{\partial L}{\partial v} = \lambda\mathbf{1} - \mu_1 - \mu_2 = 0$$

得到约束：

$$\mu_1 + \mu_2 = \lambda\mathbf{1}$$

4. 变量替换与约束转化

定义新变量：

$$z = \mu_1 - \mu_2$$

结合$\mu_1 + \mu_2 = \lambda\mathbf{1}$，解出：

$$\mu_1 = \frac{\lambda\mathbf{1} + z}{2}, \quad \mu_2 = \frac{\lambda\mathbf{1} - z}{2}$$

由于$\mu_1, \mu_2 \geq 0$，得到：

$$|z_i| \leq \lambda$$

5. 目标函数转化

将$x = y - D^Tz$代入拉格朗日函数并整理：

5.1 平方项：

$$\frac{1}{2}||x - y||_2^2 = \frac{1}{2}||D^Tz||_2^2 = \frac{1}{2}z^TDD^Tz$$

5.2 约束项：

$$\mu_1^T(Dx-v) + \mu_2^T(-Dx-v) = z^TDy - z^TDD^Tz - \lambda\sum_i v_i$$

5.3 合并所有项：

$$\frac{1}{2}z^TDD^Tz + z^TDy - z^TDD^Tz = \frac{1}{2}z^TDD^Tz - (-Dy)^Tz$$

6. 最终的标准二次规划形式

$$\begin{aligned}
\min_z & \quad \frac{1}{2}z^T(DD^T)z + (-Dy)^Tz \\
s.t. & \quad |z_i| \leq \lambda
\end{aligned}$$

转换为标准形式：

$$\begin{aligned}
\min_z & \quad \frac{1}{2}z^TPz + q^Tz \\
s.t. & \quad Gz \leq h
\end{aligned}$$

其中：

$P = DD^T$
$q = -Dy$
$G = \begin{bmatrix} I \\ -I \end{bmatrix}$
$h = \lambda\begin{bmatrix} \mathbf{1} \\ \mathbf{1} \end{bmatrix}$

7. 物理意义解释

这个转化的关键点在于：

变量替换：从原始的 $(x,v)$ 转化为单一变量 $z$
z 的意义：代表信号在各位置的修正强度
约束简化：原本的不等式约束转化为对 z 的范数约束
目标函数：
- 二次项 $\frac{1}{2}z^T(DD^T)z$ 度量了趋势的"不平滑程度"
- 一次项 $(-Dy)^Tz$ 将原始信号信息引入优化过程

这种转化使得：

问题变得更容易求解（标准二次规划）
保持了原问题的核心特征（平滑性和数据保真度的平衡）
提供了清晰的物理解释

通过这个推导过程，我们可以看到 L1 趋势滤波的优雅之处：它将一个看似复杂的非光滑优化问题转化为了一个标准的凸优化问题，而且保持了原问题的核心特征。

4. 算法实现

4.1 核心代码实现

from cvxopt import matrix, solvers, spmatrix
import numpy as np

def D_matrix(size):
    """
    构建二阶离散差分矩阵（二阶导数矩阵）的稀疏矩阵表示
  
    参数:
        size (int): 原始信号的长度
      
    返回:
        cvxopt.spmatrix: 稀疏矩阵格式的二阶导数矩阵
    """
    temp = size - 2
    value = [1, -2, 1] * temp
    r_idx = [i for i in range(temp) for _ in range(3)]
    c_idx = [i + j for i in range(temp) for j in range(3)]
    return spmatrix(value, r_idx, c_idx)

def l1_trend_filter(signal, regularizer):
    """
    L1趋势滤波算法实现
  
    优化问题:
    minimize (1/2)||x - y||₂² + λ||Dx||₁
  
    转化为标准二次规划:
    minimize    (1/2)z^T(DD^T)z + (-Dy)^Tz
    subject to  |z_i| ≤ λ
  
    标准形式:
    minimize    (1/2)z^TPz + q^Tz
    subject to  Gz ≤ h
  
    其中:
    P = DD^T
    q = -Dy
    G = [I; -I]  # I 为单位矩阵
    h = [λ; λ]   # λ 为正则化参数
  
    参数:
        signal (np.ndarray): 输入信号, shape (n,1)
        regularizer (float): 正则化参数 λ
  
    返回:
        trend (np.ndarray): 提取的信号趋势
    """

    n = len(signal)

    # 构建二阶差分矩阵
    D = D_matrix(n)
    # 构建二次规划的二次项系数矩阵
    P = D * D.T
    # 构建一次项
    q = -D * signal
  
    # 构建不等式约束矩阵G和向量h
    temp = n - 2
    G = spmatrix([], [], [], (2*temp, temp))
    G[:temp, :temp] = spmatrix(1.0, range(temp), range(temp))
    G[temp:, :temp] = -G[:temp, :temp]
    h = matrix(regularizer, (2*temp, 1), tc='d')
  
    # 求解二次规划问题
    result = solvers.qp(P, q, G, h)
    # 重构趋势
    trend = signal - D.T * result['x']  
    return trend

参考仓库：bugra/l1: L1 Trend Filtering

有绘制结果如下：

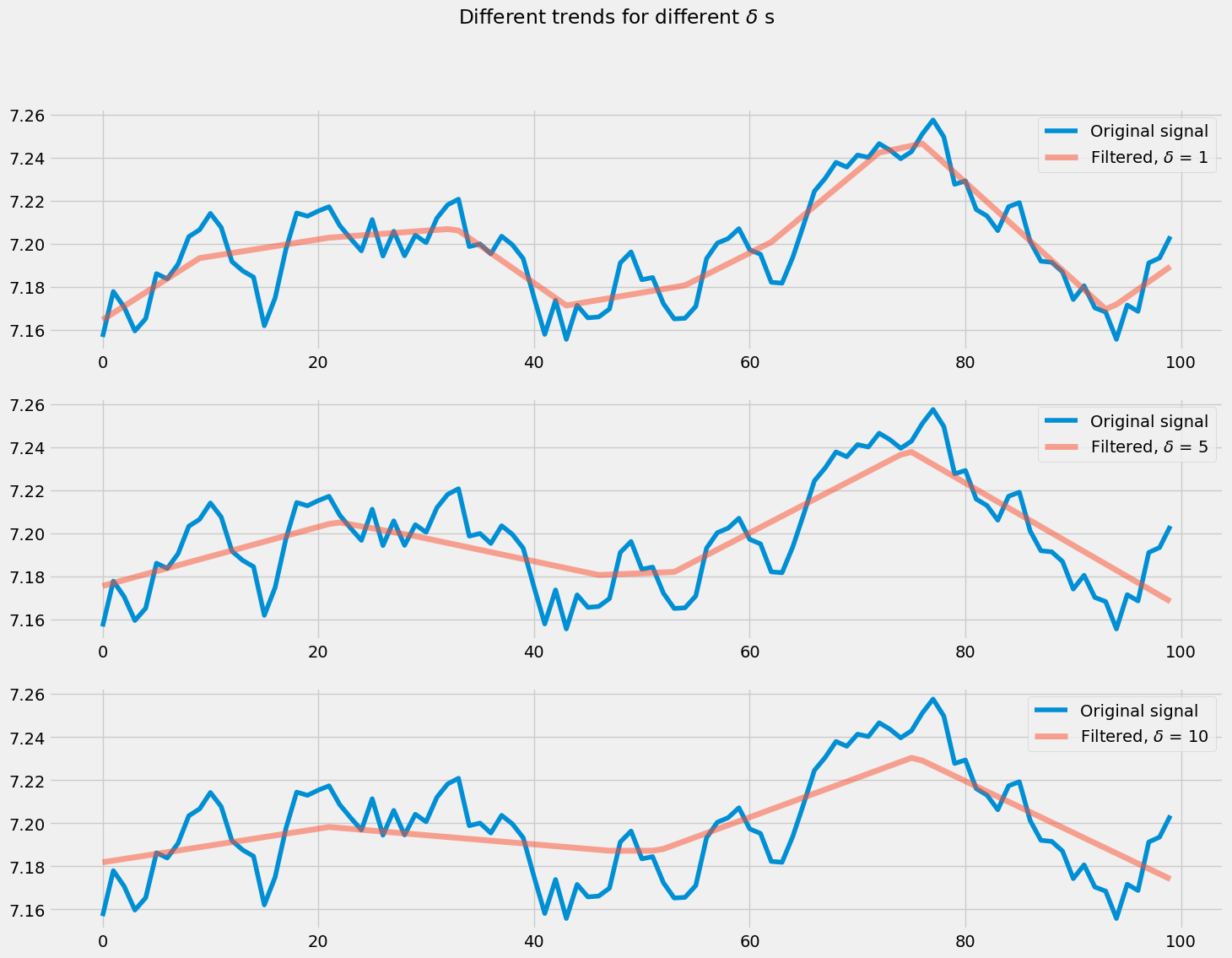
另：AI推荐使用牛顿法最小化目标函数的方法，但实测效率和结果都不够理想

有闲情逸致可以尝试
def l1_trend_filter(signal, regularizer):
    n = len(signal)
    D = second_order_derivative_matrix(n)
  
    def objective(x):
        return 0.5 * np.sum((x - signal)**2) + regularizer * np.sum(np.abs(D @ x))
  
    result = minimize(objective, signal, method='L-BFGS-B')
    return result.x