Diffusion

CLIP + VQGN + Diffusion = DALLE2

‍

扩散模型，基于分布的思想

基于规律进行扩散过程

GAN

生成器判别器迭代逼近生成目标

表现博弈对抗生成过程

cons

训练多个网络，收敛难度较大

损失难以观测

容易学习偏见（骗过判别器

多样性降低

Diffusion

DDPM 原文

Source目标存在稳定分布

通过迭代加噪音实现扩散，击碎分布

网络训练去噪过程

前向扩散 + 反向还原 = Diffusion模型

基于时刻进行迭代

（噪声作为标签）

‍

加噪过程

$\alpha_t = 1-\beta_t$ 对于每个时刻，新增噪音，保持相同的扩散幅度，有$\beta_t$从起始时刻起逐渐增大

通过$x _ { t } = \sqrt { \alpha _ { t } } x _ { t - 1 } + \sqrt { 1 - \alpha _ { t } } z _ { 1 }$ 对图像进行迭代，由$\alpha_t$控制上一时刻保留的幅度，从而控制整体扩散幅度

（串行计算墨迹难以训练，前向过程干就完事了）

‍

设计$\alpha_t$按已知项线性衰减，对上述迭代项进行递推

$$xt= \sqrt { a { t } a { t - 1 } } x { t - 2 } + ( \sqrt { a { t } ( 1 - \alpha { t - 1 } ) } z { 2 } + \sqrt { 1 - \alpha { t } } z { 1 } )= \sqrt { a { t } a { t - 1 } } x { t - 2 } + \sqrt { 1 - \alpha { t } \alpha { t - 1 } } z _ { 2 }$$

依据高斯分布乘以系数等于重采样改变方差的规则，对高斯噪声项进行化简

可得快速迭代公式有

$$x_t= \sqrt{\bar\alpha_t}x_0 + \sqrt{1-\bar\alpha_t} z_t$$

其中$\bar\alpha_t$为迭代累乘项，而$z_t$仍为标准分布

‍

去噪过程

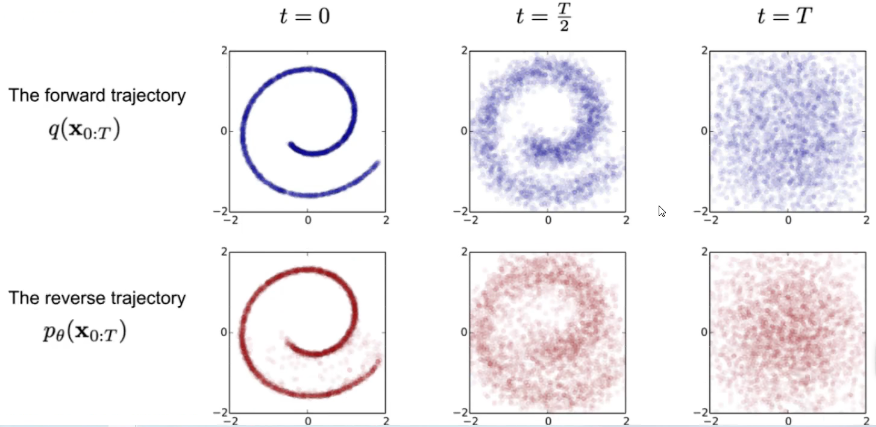
构建一个分布的还原思想$P(X_{t-1}|X_t)$

贝叶斯公式，实现逆过程

$$q ( x { t - 1 } | x { t } , x { 0 } ) = q ( x { t } | x { t - 1} , x { 0 } ) \frac { q ( x { t - 1 } | x { 0 } ) } { q ( x { t } | x { 0 } ) }$$

已知加噪的迭代方法$q(x_t|x_{t-1},x_0) = \sqrt { \alpha _ { t } } x _ { t - 1 } + \sqrt { 1 - \alpha _ { t } } z$，使用贝叶斯求逆向去噪过程

又已知$q(x_t|x_0),q(x_{t-1}|x_0)$均可由快速迭代公式前向取得，因此逆向过程的目标也是可求的

‍

有概率项服从不同正态分布

$$\begin{array}{lll}
q ( x _ { t } | x _ { t - 1} , x _ { 0 } )
& \sqrt{\bar\alpha_{t-1}}x_0 + \sqrt{1-\bar\alpha_{t-1}} z
& \sim\mathcal N(\sqrt{\bar\alpha_{t-1}}x_0, 1-\bar\alpha_{t-1}) \\
q ( x _ { t - 1 } | x _ { 0 } )
& \sqrt{\bar\alpha_t}x_0 + \sqrt{1-\bar\alpha_t} z
& \sim\mathcal N(\sqrt{\bar\alpha_{t}}x_0, 1-\bar\alpha_{t})\\
q ( x _ { t } | x _ { 0 } )
& \sqrt { \alpha _ { t } } x _ { t - 1 } + \sqrt { 1 - \alpha _ { t } } z
& \sim\mathcal N(\sqrt{\alpha_{t}}x_{t-1}, 1-\alpha_{t})

\end{array}$$

由此，我们可得$q ( x _ { t - 1 } | x _ { t } , x _ { 0 } )$的正态分布列

$$\propto \exp ( - \frac { 1 } { 2 } (
\frac { ( x _ { t } - \sqrt { a _ { t } } x _ { t - 1} ) ^ { 2 } } { \beta _ { t } }
+ \frac { ( x _ { t - 1 }- \sqrt { \bar \alpha _ { t - 1 } }x _ { 0} ) ^ { 2 } } { 1 -\bar\alpha_{t-1}}
- \frac { ( x _ { t } - \sqrt { \bar \alpha _ { t } }x _ { 0} ) ^ { 2 } } { 1 -\bar\alpha_{t}}
))$$

化简展开合并同类项，将需要计算的核心目标$x_{t-1}$整理得

$$=\exp(- \frac{1}{2}(
(\frac{\alpha _{t}}{\beta _{t}}+ \frac{1}{1- \bar{\alpha}_{t-1}})x_{t-1}^{2}
-(
\frac{2 \sqrt{\alpha _{t}}}{\beta _{t}}x_{t}
+ \frac{2 \sqrt{\bar\alpha_{t-1}}}{1- \bar{\alpha}_{t-1}}x_{0}
)x_{t-1}

+C(x_{t},x_{0})))$$

又有正态分布的分解公式为

$$\exp(- \frac{(x- \mu)^{2}}{2 \sigma ^{2}})=\exp(- \frac{1}{2}(\frac{1}{\sigma ^{2}}x^{2}- \frac{2 \mu}{\sigma ^{2}}x+ \frac{\mu ^{2}}{\sigma ^{2}}))$$

比较上下两式关系，可得均值与方差（求均值包含对$x_0$的估计）

$$\tilde{\mu}_{t}= \frac{1}{\sqrt{a_{t}}}(x_{t}- \frac{\beta _{t}}{\sqrt{1- \bar{a}_{t}}}{z}_{t})$$