AI关卡动线生成

‍

目标简述

‍

该项目初衷为如何设计一张有“魂味”的地图？——论“类魂”游戏关卡的拓扑结构在三维空间中的延拓。

在原文中，作者使用了图论的方法，通过特定规则对魂系游戏关卡进行简化，找到了让关卡具有魂味的通用规则，即关卡逻辑图的联通度。

‍

在相关的二期规划中，我们希望将关注点从抽象程度最高的图结构关系转移到更具体的地图设计。我们希望通过更好地学习低抽象层次下的关卡设计特征，从而寻找一个易用的关卡设计工具。

‍

一期动线生成工作，着眼点为玩家探索关卡的动线。数据集使用人力依据以下规则对玩家动线进行绘制：

所有玩家可以行走的路线都要至少经过一遍。
路线起始点在进入关卡的位置，终止点在击杀最终boss的篝火点或移动到下个关卡的交互点。
支线机关门，默认不存在；主线机关门存在，并且在经过全部触发所需位置之后直接打开；单向门（首次通过）和跳点默认只能单向通行。
大型空旷区域，默认区域中心是一个节点，到达这个节点之后代表整个区域探索完毕。
所有篝火点，必须被视为一个节点。
被楼梯错开的两个平面，默认为两个区域，两个区域都必须被画线经过至少一次。
画线高度需要距离地面0~50cm之内，选定画线高度之后尽量保证以后一直维持这个高度。
在满足规则1～7的基础上，画线总长度尽量最短(既重复线段长度最短)。
画线的蓝图，Speed参数设置为 8，Delta Time设置为 0.1

对于基于该规则的画线结果，我们使用打点对其进行采样，通过间距80cm的数据点连成的线采样关卡动线

‍

通过该动线数据，我们能从两个角度对数据进行分析

讨论严格遵从动线运动次序及规则的动力学动线
讨论不含运动方向及顺序信息，屏蔽重复路径的热力学路径

但目前看来尼莫大神开摆了，我们难以从抽象的动线数据中学到东西（恼

除了一个指标性的信息

确定了魂系关卡的回溯探索中，动力学与热力学路径的幂指数关系

‍

那么我也开摆，人学不会就让机器来学，我们希望能让机器实现这样一个任务，从我们绘制的数据集中学习整体动线的结构，并随机/根据上下文生成设计师所需的动线规划，协助关卡设计。

‍

数据结构

掏出我们手中现有的数据，其表现为一个(X,Y,Z)的三元组序列

X	Y	Z
-5089.32	8458.612	-1097.92
-5003.99	8450.343	-1085.51
-4925.19	8442.705	-1074.06
-4846.38	8435.067	-1062.6
-4767.57	8427.43	-1051.14
-4688.76	8419.791	-1039.69
-4609.95	8412.153	-1028.23
-4531.14	8404.516	-1016.77
···	···	···

如图所示，摘取了某张地图中的连续十个数据点。

我们获取每张图的数据为长约2k到10k的三元组序列，我们希望模型能生成符合预期特征的指定序列

‍

问题分析

那么，该问题首先为一个序列生成问题，对于此类问题，首先考虑到的都是Transformer系列模型。

但是对于这个情景，Transformer存在难以handle的问题。主要表现在Transformer对于长序列的编码的空间复杂度指数上升，以及逐项输出中时间复杂度的累计。

除此之外，动线序列还有几个需要建模的特性与约束。

首先，我们给出的序列具有固定间隔的性质，但这部分特征并非是显式的约束，需要网络自行学习。

其次，对于魂系关卡的动线生成，我们希望建模魂系关卡的“回溯探索”性质，即动线时隔特定长度回到原点的性质，即我们希望能较好地对全局空间信息实现储存。

这些需求要求我们使用某些性质更为优雅和稳定的网络尝试生成工作。

‍

模型参考

在网络设计模块之前，我们选择了两个主要参考的模型

Diffusion
- 被广泛使用的扩散式生成模型
- 适合用于学习各种分布信息
- 并通过噪声生成与概率方法对分布进行生成化的构建
Informer
- Transformer的一种变体
- 在输入层和输出层对transformer的时空复杂度进行简化
- 使用特征拼贴等方法提炼序列全局信息

一方面，我们希望使用Informer增强网络对于动线长序列的学习能力

另一方面，我们希望使用Diffusion模式来将Informer擅长的预测问题转化为生成问题

同时，避免Informer在学习时过度依赖邻域信息，对全局拟合效果较差

Diffusion 模型

Diffusion的介绍可以参考此篇笔记：Diffusion

在此简要介绍其思想

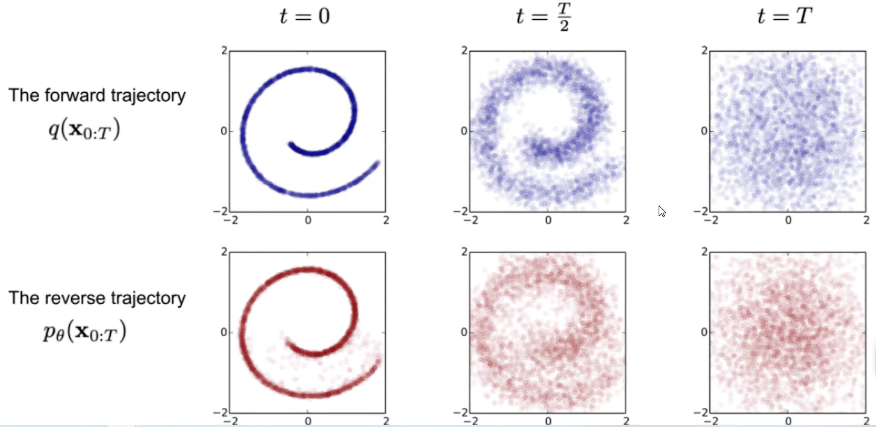
扩散模型借鉴了动力学中的扩散思想，设计了一个可学习的添加噪声，将原始分布打散的过程

在生成任务中，网络通过这个打散的逆过程，从随机的高斯噪声中进行推理，实现对目标分布的修复

‍

现有的Diffusion模型，主要被运用在图像生成领域

在图像生成问题中，Diffusion处理的是$(H\times W\times C)$空间中数据点信息的扩散

对于这样的问题，Diffusion需要使用深度学习模型进行噪声预测，综合全局的图素信息，并以此为基础推断当前时刻当前图素可能被添加的噪声。

我们所熟知的Diffusion模型多数采用U-Net的Encoder-Decoder结构来解决这个推断问题，并引入了CLIP进行文本编码，以及Attention结构的QKV操作为模型预测注入所需的信息

如图为Stable Diffusion所使用的网络结构

‍

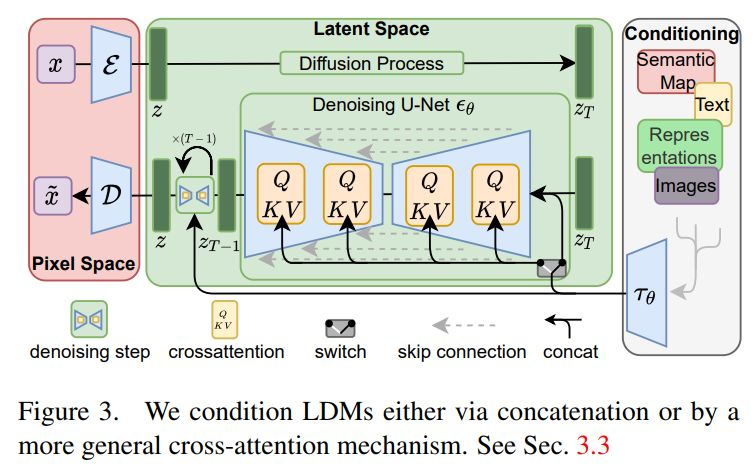
对应的，试图将Diffusion用于序列生成的我们得到了一定因地制宜的空间，即我们可以设计一个更有效且更具针对性的编解码结构来处理序列问题。

我们的序列生成问题中，实际处理的是$(N \times \mathbb R^3)$中数据点信息的扩散。其中，$\mathbb R^3$空间中的采样可以视为一个特征向量，即我们实际输入的是长为$N$，维度为$3$的特征向量序列。

即，我们需要找到一个特性合适的网络来处理一个长序列的$(N \times \mathbb R^3)\Rightarrow(N \times \mathbb R^3)$序列生成问题，即一个使用Encoder-Decoder结构的Seq2Seq模型，以区别于U-Net的Pix2Pix实现。

为此我们选取的主要参考对象为Informer

‍

Informer 模型

对于Transformer在长序列问题上的三个缺点

self-attention的时空复杂度为$\mathcal O (L^2)$
memory瓶颈，encoder-decoder栈所需的内存量为$\mathcal O(NL^2)$
transformer的decoding过程为step-by-step，因此inference所需时间过长

对此，Informer模型引入了三点改进，使得其能更好地处理长序列问题

提出 ProbSparse self-attention 机制代替 inner product self-attention，使得注意力的时空复杂度降为 $\mathcal O (L \log L)$
提出 self-attention distilling 来突出 dominating score，缩短每一层输入的长度，降低空间复杂度到 $\mathcal O((2-\epsilon)L\log L)$
提出 generative decoder 来进行输出预测，过程仅需单步前向过程，时间复杂度降低为$\mathcal O(1)$

‍

Attention: ProbSparse self-attention

依据点积注意力服从长尾分布的结论对Self-attention机制进行截断

通过采样随机Key计算注意力以度量Query的激活程度

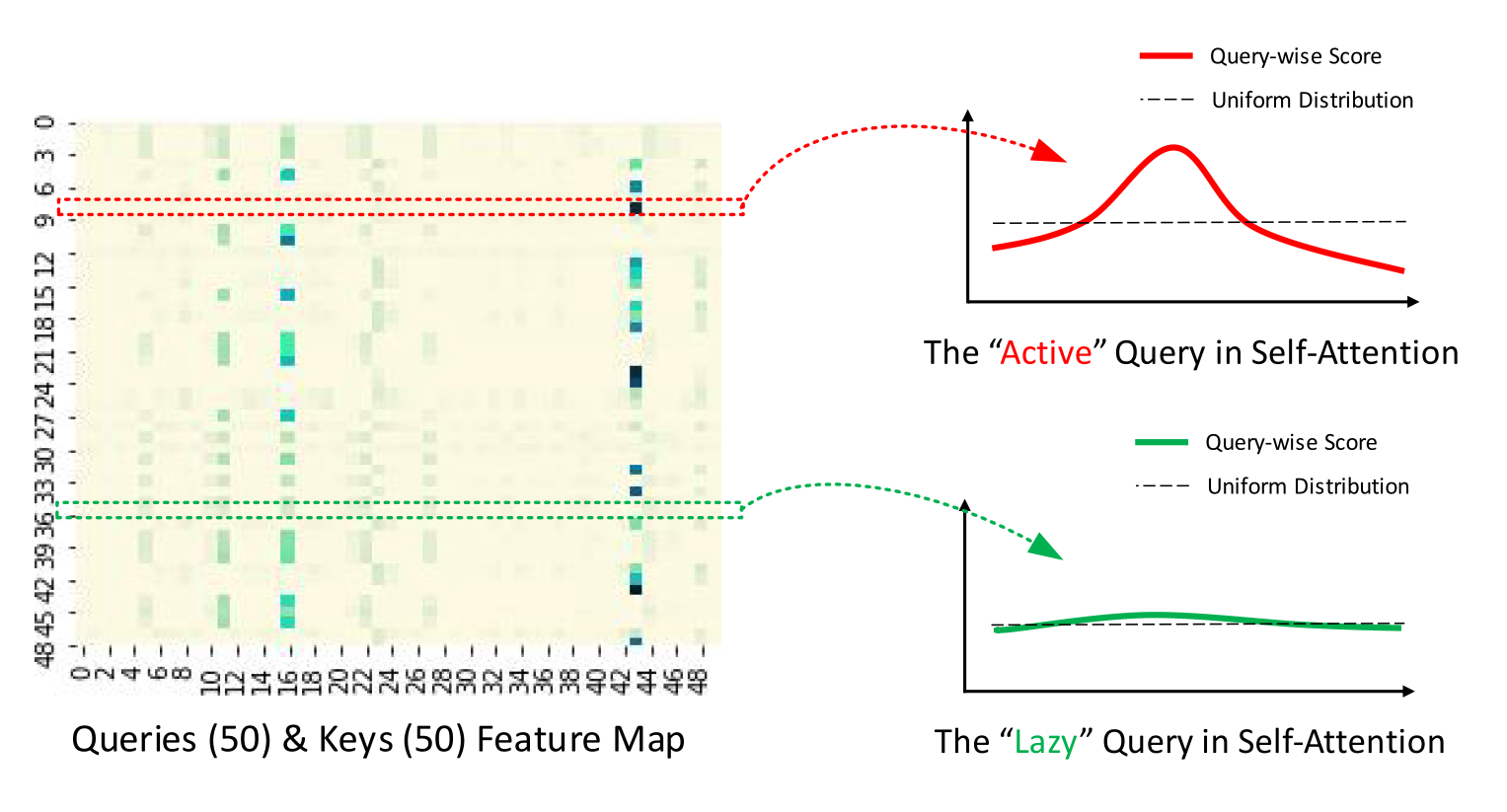
筛选高权重的$c\ln L$个 Query 用于压缩整体计算量

‍

Encoder: Self-attention distilling

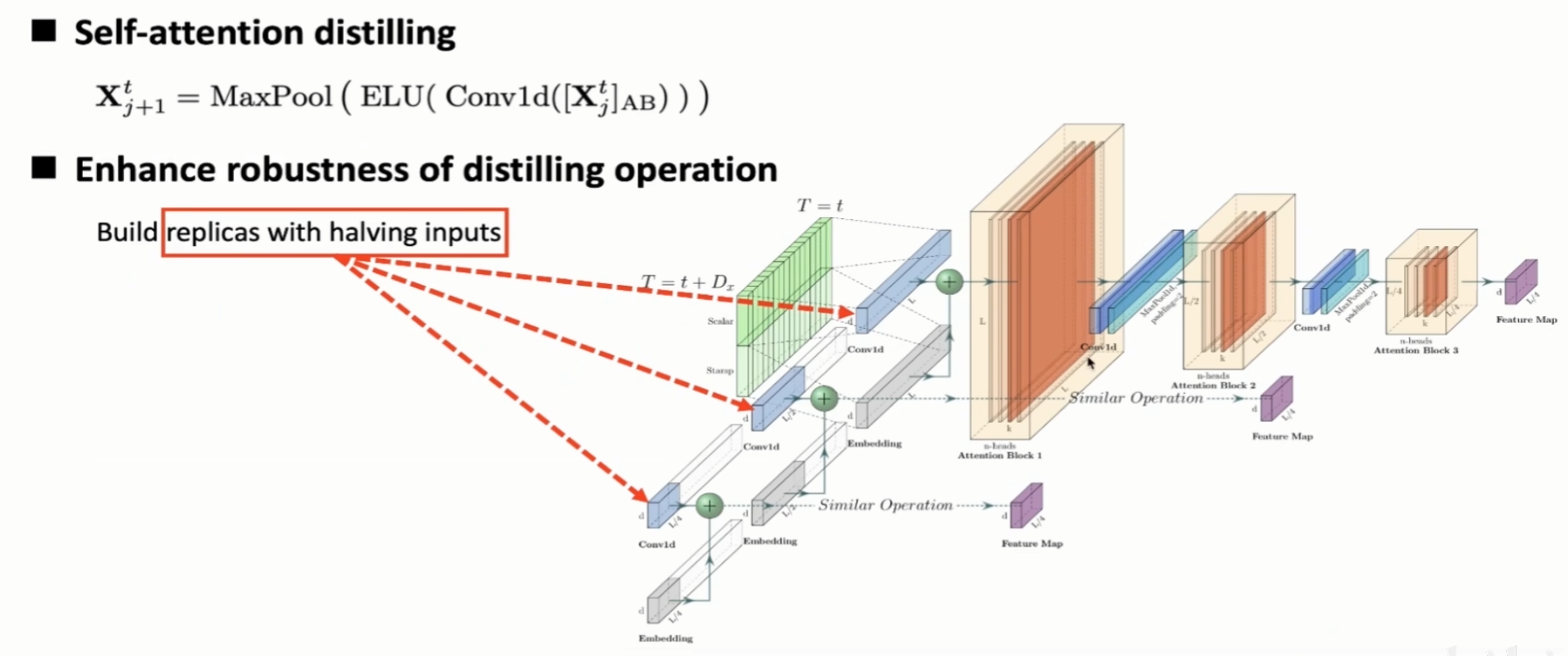
使用花活压缩 FeatureMap

有轮子就完事了，谢谢你开源人 zhouhaoyi / Informer2020

‍

Decoder: Generative inference

使用 generative inference 模式一次性解码所有元素

原文中使用$X_{de}^t = \text{Concat}(X_{\text{token}}^t,X_0^t)\in\mathbb{R}^{(L_{\text{token}}+L_y)\times d_{\text{model}}}$作为输入，前半为known sequence，后半为时间步编码的embedding（如年月日时间段、采样尺度、时间步长等）

在我们的问题中无需Known Sequence，但positional embedding部分也需要参考

‍

Autoformer

有一说autoformer对主干网络的自相关编码设计是值得参考的，btw，懒得参考了

‍

模型构建

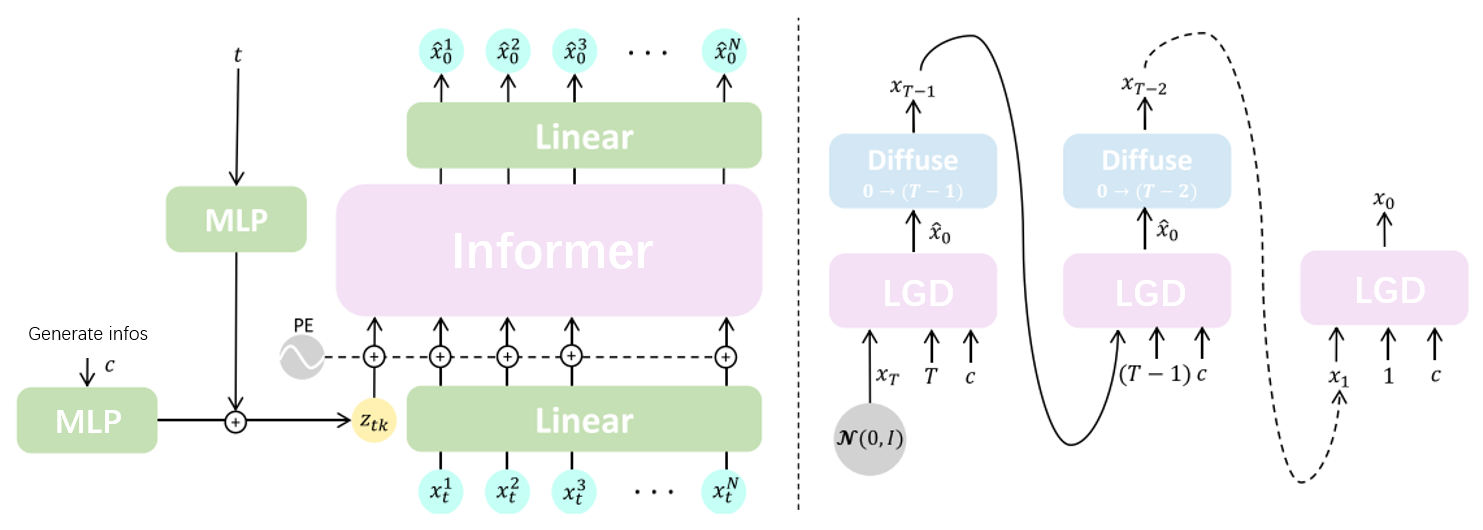
如图所示，即为我们模型的基础框架，虽然这张图是抄改来的（

该将Transformer的序列生成结构用于Diffusion噪声预测的网络嵌套结构在人体动作生成的相关领域被验证，出处为 Human Motion Diffusion Model 。该文章使用Transformer和CLIP文本嵌入对SMPL人体表示数据序列中的噪声进行修复，从而搭配Diffusion实现动作序列生成过程，并对代码进行了开源 GuyTevet/motion-diffusion-model

我们的工作也可以相对自然地建立在该工作之上。